NPN Transistor
Symbol
Information
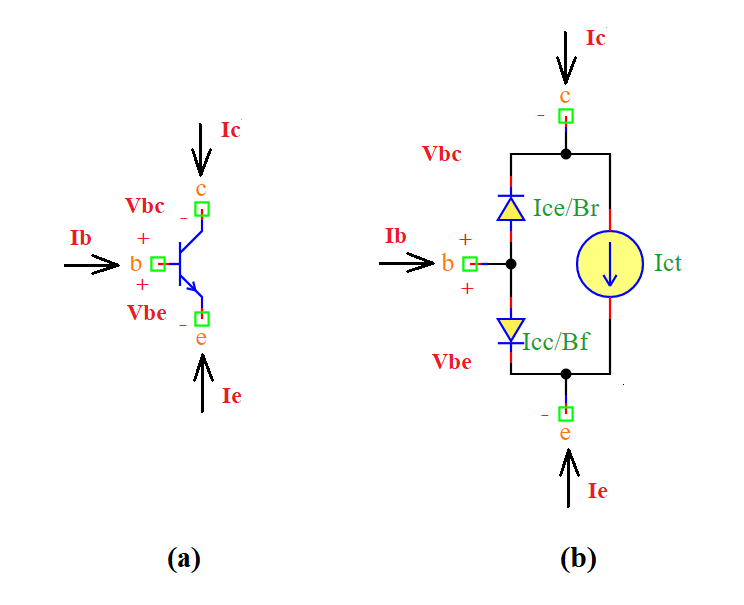
An NPN bipolar junction transistor (BJT) is a three-terminal semiconductor device used for amplification and switching applications. It consists of three regions:
Collector (c)
Base (b)
Emitter (e)
The behavior of the transistor follows the Ebers-Moll model, which describes its current-voltage relationships:
Where:
\(I_c\), \(I_b\), \(I_e\) are the collector, base, and emitter currents, respectively.
\(V_{be}\) and \(V_{bc}\) are the base-emitter and base-collector voltages, respectively.
\(I_s\) is the transport saturation current.
\(V_t\) is the thermal voltage, depending on temperature.
\(N_f\) and \(N_r\) are the forward and reverse current emission coefficients.
\(B_f\) and \(B_r\) are the ideal maximum forward and reverse beta values.
\(V_{af}\) and \(V_{ar}\) are the forward and reverse Early voltages.
\(g_{min}\) is the minimum conductance.
NPN transistors are widely used in analog and digital circuits, amplifiers, and switching applications.
Ports
c: Collector (output terminal)
b: Base (control terminal)
e: Emitter (input terminal)
Model
The NPN Transistor model implements a nonlinear behavior using the Ebers-Moll equation.
The transistor operates by controlling the current flow between the collector and emitter, based on the base-emitter voltage.
Attributes:
Vbe (signal): Base-emitter voltage.
Vbc (signal): Base-collector voltage.
Vce (signal): Collector-emitter voltage.
Ic (signal): Collector current.
Ib (signal): Base current.
Ie (signal): Emitter current.
Nf (param): Forward current emission coefficient (default: 1.0).
Nr (param): Reverse current emission coefficient (default: 1.0).
Is (param): Transport saturation current (default: 1.0e-16 A).
area (param): Device area scaling factor (default: 1.0).
Br (param): Ideal maximum reverse beta (default: 1.0).
Bf (param): Ideal maximum forward beta (default: 100.0).
Vt (param): Thermal voltage (default: 0.025 V).
Var (param): Reverse Early voltage (default: 1e3 V).
Vaf (param): Forward Early voltage (default: 1e3 V).
gmin (param): Minimum conductance (default: 1e-12 1/Ohm).
Methods:
analog(): Defines the transistor behavior using the Ebers-Moll model:
from pyams.lib import model, signal, param, voltage, current, explim
class NPN(model):
"""
NPN Bipolar Junction Transistor (BJT) model based on the Ebers-Moll equation.
"""
def __init__(self, c, b, e):
# Signal declaration
self.Vbe = signal('in', voltage, b, e)
self.Vbc = signal('in', voltage, b, c)
self.Vce = signal('in', voltage, c, e)
self.Ic = signal('out', current, c)
self.Ib = signal('out', current, b)
self.Ie = signal('out', current, e)
# Parameter declaration
self.Nf = param(1.0, ' ', 'Forward current emission coefficient')
self.Nr = param(1.0, ' ', 'Reverse current emission coefficient')
self.Is = param(1.0e-16, 'A', 'Transport saturation current')
self.area = param(1.0, ' ', 'Area')
self.Br = param(1.0, ' ', 'Ideal maximum reverse beta')
self.Bf = param(100.0, ' ', 'Ideal maximum forward beta')
self.Vt = param(0.025, 'V', 'Voltage equivalent of temperature')
self.Var = param(1e+3, 'V', 'Reverse Early voltage')
self.Vaf = param(1e+3, 'V', 'Forward Early voltage')
self.gmin = param(1e-12, '1/Ohm', 'Minimum conductance')
def analog(self):
"""Defines the transistor’s current-voltage relationships"""
Vt = self.Vt
Icc = self.Is * (explim(self.Vbe / (self.Nf * Vt)) - 1)
Ice = self.Is * (explim(self.Vbc / (self.Nr * Vt)) - 1)
Ict = (Icc - Ice) * (1 - self.Vbc / self.Vaf - self.Vbe / self.Var)
self.Ic += Ict - Ice / self.Br + self.gmin * self.Vbc
self.Ib += Ice / self.Br + Icc / self.Bf
self.Ie += -Ict - Icc / self.Bf + self.gmin * self.Vbe
Command syntax
The syntax for defining an NPN transistor in a PyAMS simulation:
# Import the model
from pyams.models import NPN
# Qname: is the name of the NPN transistor instance
# c, b, e: The connection points in the circuit
Qname = NPN(c, b, e)