Transformer

Symbol

Information

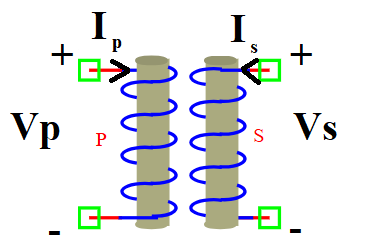
A transformer is a passive electrical device that transfers electrical energy between circuits through mutual inductance. It consists of a primary coil and a secondary coil with inductance values Lp and Ls, respectively. The mutual inductance (M) couples the two windings.

The relationship between voltage (V) and current (I) in a transformer follows these equations:

\[ \begin{align}\begin{aligned}V_p = L_p \cdot \frac{dI_p}{dt} + M \cdot \frac{dI_s}{dt}\\V_s = L_s \cdot \frac{dI_s}{dt} + M \cdot \frac{dI_p}{dt}\end{aligned}\end{align} \]

Where:

• \(V_p\), \(V_s\): Primary and secondary voltage (Volts)

• \(I_p\), \(I_s\): Primary and secondary current (Amperes)

• \(L_p\), \(L_s\): Primary and secondary inductance (Henries)

• \(M\): Mutual inductance (Henries)

Transformers are widely used for voltage conversion, isolation, and impedance matching in electrical circuits.

Ports

• p1, n1: Primary coil terminals

• p2, n2: Secondary coil terminals

Symbol description

Field	Value
Symbol.name	Transformer
Symbol.file	Transformer.sym
Symbol.directory	Basic
Symbol.referance	T
Model.name	Transformer
Model.file	Transformer.py

Model

The Transformer model implements a mutual inductor with primary and secondary windings.

The current and voltage relationships are defined based on mutual inductance and time-dependent behavior of inductors.

Attributes:

• Vp (signal): Primary voltage, defined between nodes (p1, n1).

• Ip (signal): Primary current, defined between nodes (p1, n1).

• Vs (signal): Secondary voltage, defined between nodes (p2, n2).

• Is (signal): Secondary current, defined between nodes (p2, n2).

• Lp (param): Primary inductance in Henrys (H), default is 1.0 H.

• Ls (param): Secondary inductance in Henrys (H), default is 1.0 H.

• M (param): Mutual inductance in Henrys (H), default is 0.5 H.

Methods:

analog(): Defines the mutual inductance relationship:

\[ \begin{align}\begin{aligned}V_p = L_p \cdot \frac{dI_p}{dt} + M \cdot \frac{dI_s}{dt}\\V_s = L_s \cdot \frac{dI_s}{dt} + M \cdot \frac{dI_p}{dt}\end{aligned}\end{align} \]

from pyams.lib import model, signal, param
from pyams.lib import voltage, current
from pyams.lib import ddt

class Transformer(model):
    """
    Transformer Model (Mutual Inductor)
    Defines the relationship: Vp = Lp * dIp/dt + M * dIs/dt
                              Vs = Ls * dIs/dt + M * dIp/dt
    """

    def __init__(self, p1, n1, p2, n2):
        # Signal declaration
        self.Vp = signal('out', voltage, p1, n1)
        self.Ip = signal('in', current, p1, n1)
        self.Vs = signal('out', voltage, p2, n2)
        self.Is = signal('in', current, p2, n2)

        # Parameter declaration
        self.Lp = param(1.0, 'H', 'Primary inductance value')
        self.Ls = param(1.0, 'H', 'Secondary inductance value')
        self.M = param(0.5, 'H', 'Mutual inductance value')

    def analog(self):
        """Defines the voltage-current equations for a mutual inductor."""
        self.Vp += self.Lp * ddt(self.Ip) + self.M * ddt(self.Is)  # Primary winding equation
        self.Vs += self.Ls * ddt(self.Is) + self.M * ddt(self.Ip)  # Secondary winding equation

Command syntax

The syntax for defining a Transformer in a PyAMS simulation:

# Import the model
from pyams.models import Transformer

# Tname: is the name of the Transformer instance
# p1, n1: Primary winding connections
# p2, n2: Secondary winding connections
Tname = Transformer(p1, n1, p2, n2)